Chiffre
Un chiffre est un signe élémentaire représentant une quantité, utilisé pour construire un nombre.
Les chiffres dits « arabes » désignent, dans l’usage courant, la forme occidentale (notamment européenne) des dix symboles du système de numération indo-arabe: 1, 2, 3, 4, 5, 6, 7, 8, 9 et 0. Ce système est né en Inde, avant d’être transmis à l’Occident médiéval par l’intermédiaire des savants arabes. Les formes graphiques utilisées en Europe dérivent ainsi des écritures arabes médiévales, ce qui explique leur appellation de «chiffres arabes».
D’autres signes peuvent intervenir pour représenter une quantité : par exemple le signe « moins » pour indiquer des nombres négatifs, ou la virgule pour distinguer la partie entière et la partie décimale.
Nombre
Un nombre est un ensemble de chiffres qui représente ou exprime une quantité ou un rang dans un classement.
Quantité : 0, 1, 2, 3, … → c’est un nombre cardinal ;
Rang : 1er, 2ème, 3ème, … → c’est un nombre ordinal.
Numération positionnelle
La numération positionnelle représente les nombres comme une suite de chiffres.
La position de ces chiffres correspond aux puissances successives d’un nombre b que l’on nomme base et la quantité représentée par ces chiffres est obtenue en effectuant la somme de ces puissances.
Exemple de calcul de la quantité représentée par un nombre donné en base 10, en l’occurrence le nombre 1’432 :
| 1 | 4 | 3 | 2 |
|---|---|---|---|
| 3 | 2 | 1 | 0 |
1’43210 = 1 × 103 + 4 × 102 + 3 × 101 + 2 × 100
Ici b = base = 10. Le nombre 1’432 est donc représenté en notation décimale.
Dans une numération positionnelle uniquement, la base correspond en général au nombre de chiffres à disposition. En base 10 il y a dix chiffres.
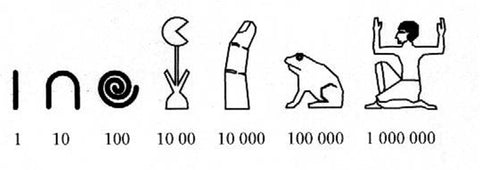
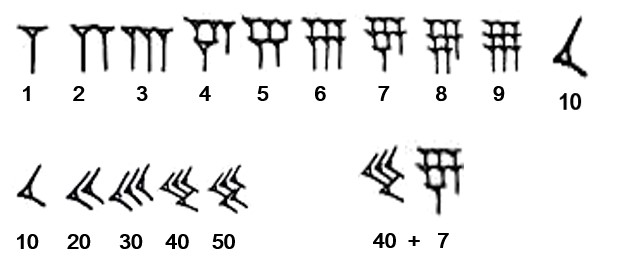
Cette opération de décomposition n’est pas possible avec la numération en chiffres romains car un tel système de numération n’est pas positionnel. Avec la numération en chiffres romains, en effet, la position des chiffres (ou leur rang dans la série de chiffres composant le nombre) ne correspond pas aux puissances successives d’une base.
Autres exemples de systèmes de numération non-positionnels :